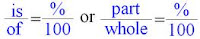Introduction:-
In this lesson let me help on how to calculate pi ╥ (sometimes written pi) is a mathematical constant whose value is the ratio of any circle’s circumference to its diameter in Euclidean space; this is the same value as the ratio of a circle’s area to the square of its radius
* pi is a dimensionless quantity.
* pi is an irrational number.
* pi is an transcendental number.
* Decimal notation of pi is 3.141593.
* Fraction notation of pi is [ 22/7.]
There are many formula's in the mathematics and science, which engage pi and pi calculation. This also helps us on examples of symbols
In this lesson let me help on how to calculate pi ╥ (sometimes written pi) is a mathematical constant whose value is the ratio of any circle’s circumference to its diameter in Euclidean space; this is the same value as the ratio of a circle’s area to the square of its radius
* pi is a dimensionless quantity.
* pi is an irrational number.
* pi is an transcendental number.
* Decimal notation of pi is 3.141593.
* Fraction notation of pi is [ 22/7.]
There are many formula's in the mathematics and science, which engage pi and pi calculation. This also helps us on examples of symbols